Motion in One Dimension with Air Drag

Purpose: 

The purpose of Motion in One Dimension with Air Drag is to analyze how a changing force will affect motion in one dimension.

Introduction: 

Up to this point in the class, we have only discussed problems that involve constant forces. But what happens if a changing force is applied to an object (e.g. a force that has a changing magnitude over time)? This would affect the acceleration that the object was experiencing, it would begin at an initial value and the function would gently reach a=0 once terminal velocity is reached. Calculus provides a method to determine the way in which the acceleration and velocity of the object are changing. In this lab a spreadsheet will be used to calculate these changing values. Two basic relationships can be used to analyze the object:

V_new = V_old + a_avg * ∆t

Where V_old = previous value of velocity, a_avg = value of acceleration at the midpoint of the time interval

1)      Using unit analysis, the above equation is verified:

(m/s) = (m/s) + (m/s^2)*(s)

(m/s) = (m/s) + (m/s)

(m/s) = (m/s)

2)      Why do we use a_avg in equation 1?

The Since the acceleration is changing at every moment in time, we calculate the value of our acceleration in the average of the time interval for every ∆t.

3)      Come up with an analogous equation relating y_new to y_old.

y_new = y_old + v_avg*(∆t) + (a_avg/2)*( ∆t^2)

or

y_new = y_old + v_avg(∆t)

4)      What is the benefit of choosing a small ∆t?

The smaller the value of the time interval we choose for ∆t, the less dramatic the overall change in acceleration during that time interval will be, resulting in an estimated value much closer to the actual value.

Because acceleration s the result of all forces acting on the object, all forces need to be specified. In this problem, the drag force will be assumed to be the first power of the velocity and can be written as:

F_D = -kv

Where k is a proportionality constant

1)      Draw a detailed motion diagram for the object falling down. Pictured in fig 1 is the motion diagram of an object experiencing an increasing drag force.

fig 1

a)      Pictured in fig 2 is the force diagram of the object, assuming terminal velocity was reached.

fig 2

      From Newton’s Second Law, it is known that an object of mass (m), will undergo acceleration as a result of the sum of all forces acting on the object.

F_net = m*a

Where:

F_net = F_D – F_W

m*a = (-kv) – (m*g)

Solve for acceleration:

a = ((-kv)-(m*g))/m

b)      Taking into consideration that we are looking at terminal velocity, let v_t = terminal velocity, and take a = 0. Solve for k:

0 = ((-kv_t)-(m*g))/m

0 = (-kv_t)-(m*g)

(-kv_t) = (m*g)

k = -((m*g)/ v_t

c)      Substitute this value for k back into the expression for Newton’s Second Law:

a = ((-(-((m*g)/ v_t )*v)-(m*g))/m

a = m*(((g/ v_t )v)-g)/m

a = (((g/ v_t )v)-g)

a = g*((v / v_t )-1)   or equivalently,

a = -g*(1- (v / v_t ))

2)      Next, open the file entitled Air Drag. Describe what the Spreadsheet is calculating.

a)      What are the initial values that are assumed in the spreadsheet?

y₀ = 1000 m

v₀ = 20 m/s

a₀ = -14.7 m/s²

b)      What is v – halfstep?

v – halfstep is the velocity calculated in the average of the time interval ∆t.

c)      What is a – halfstep?

a – halfstep is the acceleration calculated in the average of the time interval ∆t.

3)      Draw graphs of position vs. time, velocity vs. time, and acceleration vs. time for the object assuming no air drag. Pictured in fig 3 are the estimates of the position, velocity, and acceleration vs. time graphs.

fig 3

Now assume air drag and draw estimates of what the graphs would look like. Pictured in fig 4 are my personal estimates of what the same graphs would look like if the object was also experiencing an increasing force, opposite the direction of motion.

fig 4

4)      Create graphs in the graphical analysis software by selecting the data ranges we have calculated. Compare the predicted graphs to the graphs made in the graphical analysis software. How are they similar, how are they different? Pictured in fig 5-7 are the acceleration vs. time, velocity vs. time, and position vs. time functions of the object undergoing drag force -kv.

fig 5

fig 6

fig 7

The graphs that were predicted were fairly accurate. The Position vs. time graph starts off parabolic but it eventually reaches a constant slope, therefore a constant speed. The velocity vs. time graph starts off positive and it decreases in speed, changes direction, then its slope increases to zero, meaning its acceleration tapers off to zero. The object has an initial acceleration but, as drag increases, the value of acceleration heads to zero.

a)      If a = -g*(1- (v / v_t )) when F_D = -kv, predict what the acceleration will look like if   F_D = kv²

F_net = F_D – F_W

m*a = (kv²) – (m*g)

a = (kv²)/m – (m*g)/m

assume terminal velocity (a=0)

0 = (kv_t²)/m – (m*g)/m

0 = kv_t² – mg

kv_t² = mg

k = (mg)/(v_t²)

plug it back into acceleration equation

a = (((mg)/(v_t²))*v²)/m – (m*g)/m

a = ((mg)/(v_t²))*v²) – (m*g)

a = m*((g/v_t²)*v² – g)

assuming terminal velocity

0 = m*((g/v_t²)*v² – g)

0 = (g/v_t²)*v² – g

0 = g*(v² /v_t² – 1)

Therefore

a = g*(v² /v_t² – 1)

5)       After copying the spreadsheet, it was modified. The acceleration was changed to the new formula for |kv^2|. Pictured below are the spreadsheets with formulas and data for a drag force = 0, Drag force  = -kv, and drag force = |kv^2|.

Fig 9
(fd = 0 spreadsheet data)

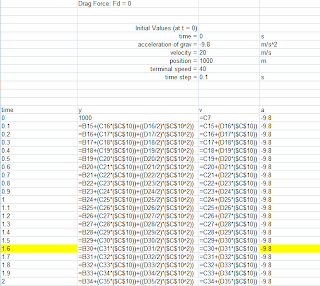Fig 8
(fd = 0 spreadsheet formulas)

Fig 10
(fd = -kv spreadsheet data)

Fig 11
(fd  = -kv formulas)

Fig 12
fd = |kv^2| data

Fig 13
fd = |kv^2| formulas

6) Taking the time to be the independent values, and the position or y value to the independent variable, graphs of all three drag forces were plotted on one graph. Pictured in Fig 14 are the position vs. time graph of fd = 0, fd = -kv, and fd = |kv^2|.

Fig 14

In addition, the velocity vs. time graphs of all three drag forces were also to be plotted. Pictured in Fig 15 are the velocity vs time graphs for all 3 drag forces.

Fig 15

In analyzing drag forces that had varying degrees of intensity, one can now make a reasonable assumption about how a changing force will effect the motion of an object. If an object experiences a constant force, and thus constant acceleration, the velocity will continue to change in a linear fashion with the slope equal to its acceleration. If there is a force that is proportional to the speed of an object opposing motion, the acceleration will have some initial value, and gently approach zero. The velocity of this object will continue to increase until the object no longer accelerates at which point terminal velocity was reached in this lab. The position function will start off parabolic with the slope gradually becoming linear. The main source of error in this lab would be entering formulas into excel incorrectly. Our group had a few issues with getting the numbers to match with the values as they would be expected.