To use the ballistic pendulum to determine the initial velocity of a projectile using conservation of momentum and conservation of energy.
Equipment:
Ballistic pendulum, carbon paper, meter stick, clamp, box, triple beam balance, plumb
Introduction:
In this experiment, a steel ball will be shot into the bob of a pendulum and the height (h) to which the pendulum bob moves, as shown in fig 1, will determine the initial velocity (V), of the bob after it receives the moving ball.
 |
| fig 1 |
If we equate the kinetic energy of the bob and ball
at the bottom to the potential energy of the bob and ball at the height, h, that
they are raised to, we get:
(
K.E ) bottom = ( P.E)top
½
( M + m ) V² = ( M + m ) g.h
where M is
the mass of the pendulum and m is the mass of the ball. Solving for V we get:
V = √ 2gh ……………. ( 1 )
Using conservation of momentum we know the momentum
before impact (collision) should be the same as the momentum after impact.
Therefore:
Pi
= Pf
or
mv0
= ( M + m) V …………… ( 2 )
where v0 is the initial velocity of the
ball before impact. By using equations (1) and (2) we can therefore find the
initial velocity, v0, of the ball.
We can also determine the initial velocity of the
ball by shooting the ball as above but this time allowing the ball to miss the
pendulum bob and travel horizontally under the influence of gravity. In this
case we simply have a projectile problem where we can measure the distance
traveled horizontally and vertically (see Figure 2) and then determine the
initial velocity, v0, of the ball.
Fig 2 shows the procedure for letting the steel ball miss the pendulum and follow its projectile motion trajectory.
Starting
with equations:
∆x
= voxt + ½axt² ……………… ( 3 )
∆y
= voyt + ½ayt2 ……………… ( 4 )
You should be able to derive the initial velocity of
the ball in the horizontal direction (assuming that ∆x and ∆y are known).
Include this derivation in your lab report.
Procedure, part one (determination of initial velocity using conservation of energy):
1) With the apparatus on the edge of the table and clamped down, make sure that the ballistic pendulum is level with the bubble level. In order to get the gun ready to be shot, pull back on the steel ball until the trigger is engaged. This will make sure the spring is compressed a known amount, therefore the ball will have an equal initial velocity each time it is fired.
2) Before firing, it is crucial to make sure the pendulum is at rest. Once it has stopped swinging, pull the trigger, and the ball will be shot into the pendulum and the combined masses will raise a definite height (h) and stop in a given notch.
3) Now shoot the steel ball into the cylinder nine times, and record the number of notches that the pendulum raises to each time. Taking the mean value of these nine trials will give us the average height (h) that the pendulum raised. Now take raise the pendulum bob to the notch that is the average value and take the measurements as pictured in fig 3.
 |
| fig 3 |
4) Carefully remove the pendulum from its support and weigh the masses of the pendulum, and the steel ball separately. Replace the pendulum and carefully adjust the thumb screw.
Pendulum mass = 0.2153 kg
Steel Ball mass = 0.0567kg
5) From this data, calculate initial velocity using equations one and two.
Using formula one to solve for final velocity, we
obtain:
V = √
2gh
V = (2 * 9.8 m/s2 * 0.11 m)1/2
V = 1.48 m/s
Plugging this value into equation two to solve for
initial velocity, we get:
V0 = (MV/m) + V
V0 = (0.2153 kg * 1.48 m/s)/ 0.0567 kg +
1.48 m/s
V0 = 7.11 m/s
Procedure, part two (determination of initial velocity from measurements of range and fall):
1) Move the pendulum bob up on the rack so that it will not be in the path of the steel ball. Clamp the apparatus to the table and aim it out towards the floor. With one person watching to see where the ball strikes, this reference point is used to place the piece of carbon paper on the ground, which will aid in obtaining exact measurements.
2) Shooting the ball about 5 separate times, we can take the average distance that the ball traveled in measuring its trajectory. Pictured in fig 4 was the method that we had used to measure the horizontal distance traveled.
 |
| fig 4 |
After taking the average, we can now calculate average initial velocity using equations 3 and 4.
∆x = voxt + ½axt²
where ax = 0, and ∆x = 2.91 m
2.91 m = voxt
2.91/vox = t
Plug this into the equation for y
∆y = voyt + ½ayt2 where ∆y = -1.02 m, voy = 0, ay = -9.8 m/s2
, and t = 2.91/vox
-1.02 m = (1/2)(-9.8 m/s2)( 2.91/vox)2
Vox = (40.6)1/2
Vox = 6.37 m/s
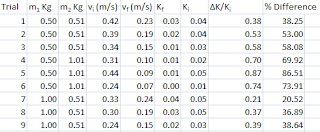
3) Calculate the percentage difference between the results obtained in part one and part two.
 |
| percentage difference |
Conclusion:
In completing The Ballistic Pendulum, one would be better able to understand how to determine the initial velocity of a projectile using the conservation of momentum and the conservation energy. I learned that we can determine, within a rough estimate, the average initial velocity of a projectile if both masses are known, or if its projectile path is measured. There were many potential sources of error in this lab which include the following:
1) There was friction present in the system as the pendulum bob swung upwards.
2) The steel ball had a varying initial velocity each time it was fired.
3) Certain distances may not have been measured in entire accuracy.
4) The spring loaded trigger may have been pulled back further for a trial or two.
An educated guess would be that part one would yield the more accurate result. Since the apparatus has a varying initial velocity each fire, part two would be less accurate in the fact that we had to measure large distances, and it may not have been so precise.